Learning System

This page reflects my/our idea about the Learning system. It consists of a few interdependent systems for functions of estimation, inference and storage.

Glucose level estimation

Example of glucose level estimation.

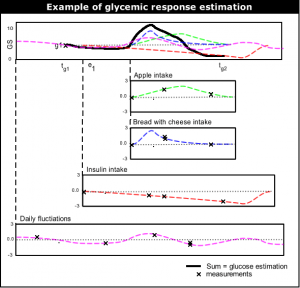
The most top-level functioning of the learning system is to give near future glucose level estimation. The current glucose level estimation is done by (1) taking the last glucose measurement, and then (2) adding up the typical glycemic response (glucose rise/fall) of all events since the last measurement.

The function f(t)

The glycemic response of each event is modelled in terms of a glucose rise/fall in function of time: f(t). Time real time t is mapped to discrete intervals of 15 minutes. Event types are split into distinct categories (see below). For computational conveniance, each event type category c is modelled by a function f_c(t), and each concrete individual event type is modelled as transformation of that function using parameters a and b: a*f_c(b*t).

• Food intake. Usually has a positive glycemic effect. It appears to be modelled as:

<math>f(t) =

a    * exp \left [ \left ( \frac{t-b }{0,667*b} \right )^2 \right ] +

(a/2) * exp \left [ \left ( \frac{t-2b}{0,667*b} \right )^2 \right ] + (a/4) * exp \left [ \left ( \frac{t-3b}{0,667*b} \right )^2 \right ] </math>

• Insulin intake. Usually has a negative glycemic effect.

• Stress level.

• Time of the day, because glucose levels structurally differ during the day.

• Health status.

• For pregnancy diabetes: progress of pregnancy. Its hormone decreases insulin sensivity.

• Other event types.

g2 Estimation

As told above, the estimate for future moments in time is done by taking the last glucose measurement and adding the sum of glycemic responses of events. If g1 at <math>t_{g1}</math> is the last glucose measurement, g2 at <math>t_{g2}</math> is the glucose level to be estimated, and <math>(e_1,e_2,...,e_n)</math> events that have influence on g2. <math>(f_1,f_2,...,f_n)</math> are the estimated functions of the events. <math>(t_1,t_2,...,t_n)</math> are the (start) times of each events. Then the glucose prediction g2 at <math>t_{g2}</math> is:

<math>g2_{estimate}(t_{g2}) = g1 + \sum_{k = 1}^n \left ( f_k(t_{g2}-t_k)-f_k(t_{g1}-t_k) \right )</math>

On events

Like told above, the term 'event' can be things like apple intake. Our definition is broader then that: events can also be composite. A composite event is a set or cominbation or multiple single events. Why use composite events? Because, for example, eating different food types combined leads to a different glycemic response then the sum of individual foods. Eating certain food types nullify the effect of other foods. Another positive thing about compositive events is that it decreases the amount of events in the sum of g2_estimate (see above). Less summation means less uncertainty about the estimate.

Creation of a new event type

What needs to be done when a new event type is created, for example when a user eats something new or gets new insulin therapy? The first the system needs to create is an a priori estimate of f(t). This is called the a priori function. For food, this would be based on carbonhydrate count. For insulin, this would be done by entering medicine information. A better a priori f_prior(t) means the system needs less training time to estimate the real function f(t). When evidence arrives in the form of a sample, an a posteriori f_post(t) is formed that esimates the real function f(t). A sample is an observation value of f(t) at some t. More evidence/samples means a better a posteriori f_post(t).

In other words:

• Better prior knowledge (carbonhydrate count etc) leads to a better f_prior(t)
• A better f_prior(t) leads to a better f_post(t)
• More samples leads to a better f_post(t)
• A good f_post(t) means it is close to the real f(t)

Significance of good f_prior(t)

In our case, we will see that the samples are estimations too. Later on, we will conclude that better f_post(t) functions lead to better estimations of samples. In the 'bigger picture', this means that bad-quality f_prior(t)'s implicates inititally bad-quality f_post(t)'s, which in turn implicate intially bad-quality samples, leading to initially slow progression of inference. This is important to know, because quality f_prior(t)'s are VITAL to fast initial inference. Concretely said, good a priori functions will decrease the startup time significantly, maybe from months to just weeks or days.

Generating of a f_prior(t) or its prior parameters

So what are the steps of creating f_prior(t) for certain event types? For...

• Food intake, calculate the a and b paramaters (for information about these parameters, see above). [Mapping of Carbonhydrate count to a and b parameters to be added]

• Insulin intake. [To do]

• Stress level. [To do]

• Time of the day. [To do]

• Health status. [To do]

• Other event types. [To do]

Attributes of event types

Summarizing what we have said above, each event type has the following attributes:

• An a priori function f_prior(t)
• A (initially empty) set of samples, each a tuple {t,dg} with t=time and dg=delta-g, the glycemic response.
• An a posteriori function f_post(t)

The following section will describe the process of computation of f_post(t).

Bayesian Inference

So how does the system calculate f_post(x)? And how are the samples created?

Statistical nature of the function f(t)

In the texts above, we wrote about the glycemic response functions f(t), like f_prior(t) and f_post(t) functions. For inference reasons, because we are using bayesian inference, we must describe the problem in terms of statistics. Following this viewpoint, one could say at t, there is a mean estimated value and variance value indicating the mean error. This way we describe each function in terms of a normal (Gaussian) distribution. So each point t doesnt map to just one value, but to two: mean <math>\mu</math> and squared variance <math>\sigma^2</math>, written as <math>f(t) = \mu_t \pm \sigma_t^2</math>. The variance <math>\sigma_t^2</math> is a static value, and we assign some reasonable value to it, defined by the event type (like 3 for food or something). The mean value μ is the to be estimated variable, or the unknown parameter θ. This unkonwn paramter θ is exactly (and only) thing we need to learn for each t. θ is where its all about. And each event type has a whole line of θ's because it has one θ for each t. To be able to compute θ, we need to see it as a normal distribution too: <math>\theta = \mu_\theta \pm \sigma_\theta^2</math>.

And now we can use our prior and posterior functions. The f_prior(t) function defines the prior mean values <math>\mu_\theta \pm \sigma_\theta^2</math> for each t for each event type. Through bayesian inference, which functions we will soon explain, we will compute the <math>\mu_\theta \pm \sigma_\theta^2</math> for each t for each event type: the _post(t) function.

Using samples, we can use Bayesian inference to compute μ_post for each t. This will be explained in the following section.

Learning System, ignite your engine!

Assume that with formula's described in above sections, we are given a group of event types, each event type has a f_prior(t). Additionally, each event type has an initially empty set of samples <math>\{s_1 s_2,...,s_n\}\!</math>.

Assume the last glucose measurement was g1 at t_g1 with value g1. Now we do a new glucose measurement g2 at t_g2 with value g2. The set of events that have impact on glucose level g2 is <math>\{e_1,e_2,...,e_n\}\!</math>. Each event e_k has an event type with attributes described above, a timestamp t_ek, and a multiplicity indicator.

1. Calculate helper variable a

The first thing we calculate is the helper variable a. Each event i has a <math>f_i(t_{g2}-t_{ei}) \to \mu_{\theta,post} \pm \sigma_{\theta,post}^2\!</math>. If <math>\mu_i \pm \sigma_i\!</math> are (synonyms of) these posterior mean and variance values for event i, and (g2-g1) is the measured glucose rise/fall, then:

<math>a = \frac{(g2-g1)-(\mu_e1+\mu_e2+...)}{\sigma_1^2+\sigma_2^2+...}\!</math>

2. Update event knowledge

This step is looped trough all events i in <math>\{e_1,e_2,...,e_n\}\!</math>. Furthermore this loops through composite events <math>{e_a+e_b+e_c,e_d+e_e,...}</math> which are combinations events that happen at the same time. Time t is measured in intervals, so the chance that events happen at the same t is quite big.

2a. Calculate subsample <math>s_i</math> of <math>e_i</math>

Now we can calculate the subsample <math>s_i</math> for event k. What is this? The user did a new glucose measurement, and the system sees the difference in glucose level (g2-g1): in statistical terms, (g2-g1) is our new composite sample <math>s_{tot}</math>. This sample is actually a composite sample, because it is caused by the sum of all events <math>\{e_1,e_2,...,e_n\}\!</math>. So to add a sample to each single event, the system needs to divide this composite sample into subsamples, one for each event. Using our calculated helper variable a, we do this using this simple formula:

<math>s_i = \mu_i + a \times \sigma_i \!</math>

For proof, ask me.

While <math>s_i\!</math> is the most likely subsample of <math>s_{tot}\!</math>, it is still an estimation. How well it comes close to the 'real' value of <math>s_i\!</math> depends on the precision of the posterior variables <math>\mu_{\theta,post} \pm \sigma_{\theta,post}^2\!</math>. Like written above, the initial values of these 'a posteriori' variables are close to the 'a prior' variables, so it can't be pressed enough that these prior variables are important.

(Maybe an improvement would be to store the supersample in combination with the event types somewhere. Old supersamples can then be used again to compute even more likely posterior distributions. This whole routine can then be iterated of all glucose measurements)

2b. Add <math>s_i</math> to <math>e_i</math>'s sample set

Now that we have a new subsample, we can add it to its sample set: <math>\{s_1 s_2,...,s_n,s_i\}\!</math>. Now this is used to update the posterior values of i.

2c. Update posterior values

If <math>\sigma_t^2</math> is the static event variance, and <math>\bar s</math> is the mean value of <math>\{s_1 s_2,...,s_n,s_i\}\!</math>, then:

<math>\mu_{\theta, post}=\frac{\sigma_t^2\mu_{\theta, prior}+n\sigma_t^2 \bar s}{\sigma_t^2+n\sigma_{\theta, prior}^2}</math>

<math>\sigma_{\theta, post}^2=\frac{\sigma_t^2\sigma_{\theta, prior}^2}{\sigma_t^2+n\sigma_{\theta, prior}^2}</math>

For proof, see "Morris H.DeGroot and Mark J.Schervish. Probability and Statistics, third edition: blz 330".

2d. Repeat

Repeat 2a-2c for each i, and all worthfull composites.